| 【明慧網二零二一年十二月十三日】(接前文) 空間認知的相對性 大家可能在前面的內容中發現了一個特點,就是一旦觀察者所處的視野基點發生改變,宇宙空間中用於辨別方位的上下左右全都不一樣了。就像佛家的卍(萬)字符,裏面的筆劃,這麼看是橫著的,那麼看是豎著的;不過,即使轉過來,當橫著的筆劃變成了豎著的,豎著的變成了橫著的,卍還是卍。單從圖象上看,卍字符本身各部位結構概念的相對性保證了圖形的恆定不變。 可能有的朋友感受到了卍字符玄奧非凡,但又覺得對其內涵了解得不太清晰,是這樣的。佛國世界、宇宙十方的很多不同層次的法理都只可意會而難以言述其點滴。這是人類的思維結構和語言的內在容量造成的,筆者這裏也只能儘量以文字在最淺顯的層面上簡單表述一點基礎的藝術理論。 蘇軾在《題西林壁》裏寫道:「橫看成嶺側成峰,遠近高低各不同。」人們對於空間的認知,其實始終具有一種相對性。 這就好比站在南極的人所說的上方與站在北極的人說的上方完全相反。同樣道理,哪怕是兩人面對面,每個人的左手在對方看來都是右邊那隻手,而右手從對面看則是左邊的手。 懂得這種相對性在繪畫上是很重要的,大型繪畫中最常見的天頂畫就是建立在多視角構圖基礎上的一種藝術形式。對於一幅大型天頂畫,如果進入可視範圍的角度是開放的,站在東南西北各方向的觀眾自然都不希望自己看到的是一幅倒著的畫。因此,藝術家在運用透視法構圖時,就必須設身處地地為位於各個方向的觀眾考慮,盡可能從不同的視角思考如何建構出讓每個位置的人都能看明白的作品。 
圖例:意大利畫家科雷吉歐(Antonio da Correggio)為帕爾馬主教座堂(Duomo di Parma)創作的天頂畫《聖母升天圖》(Assunzione della Vergine),作於1526年~1530年。 |
透視學就是建立在視覺空間相對性的基礎之上的:當一個物體離人很近,哪怕一片小小的樹葉在視野中都會顯得很大;而當事物在遠處時,即使一座山,也會相對顯小。所謂「一葉障目,不見泰山」就是源於這種規律,在透視學中稱之為「近大遠小」,這也是透視學的基本原理之一。 不過,這些原理都有一個前提:它們只是在人類身處環境裏的透視規律,一旦超出這個範圍就不一定是這樣了。比如早晨的太陽顯得很大,而到了中午太陽則顯得小,這就完全不符合透視學裏近大遠小的規律;再比如由於時空彎曲和光的運行狀態等諸多原因,一些遙遠的天體在天文望遠鏡裏還會顯示出類似近小遠大的虛像狀態。也就是說,人的理論只在人的層面內有效,而超出那個層次時,就是另一番天地了。 視野的遠近大小不僅牽扯空間,甚至還與人對時間、速度等因素的感知相關。人的視覺機制有一個特點,就是在擁有廣闊的視野時,遠處快速移動的東西會顯得較慢;而當人越靠近或者身臨其境時,眼睛看到的運動則顯得更快。舉個例子,較慢的手槍子彈速度大約每秒鐘三百米,但人眼完全跟不上這個速度;而運載火箭升空後的速度是用千米/秒來計算的,人眼卻能輕鬆跟上比子彈快十幾倍的火箭飛行速度,甚至還感覺火箭飛得挺慢。這裏就有個不同參照空間範圍內對時間感受相對性的問題。 不同範圍的視野還能引發人在認知上的差異。比如以前有許多人認為在地上走直線只會越走越遠,但通過衛星遠離地面後拍攝照片,能看見地球是圓的。所以如果一直走直線,最後還是會繞一圈回到出發點。雖然生活中沒幾個人能感覺到腳下的地是圓的,但在遼闊的地面,直線其實是一種曲線。也就是說,當人身處某個局部的環境之中時,與整體的認知概念差異很大。 位相幾何學(Topology)裏有個經典結構叫莫比烏斯環(Möbius strip),用一根紙條旋轉半圈後再把兩端粘上就能做出來。我們假設有一個這樣的環很長,長到一眼看不完全部,而只能看到局部,人們就會根據觀察到的情況認為它有正反兩個面;可是,當人了解到整體情況後就會發現:原來兩個面都是一個面啊!在這裏,「二」是「一」的局部,是不是很讓人感慨? 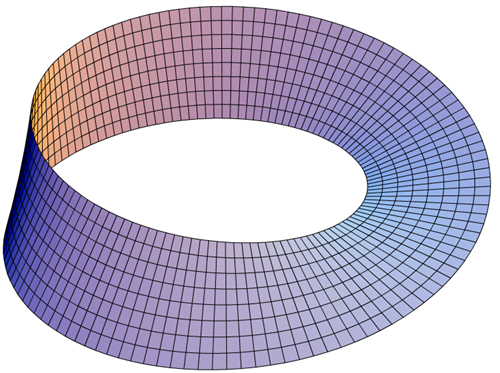
圖例:莫比烏斯環,是一種只有一個表面和一條邊界的曲面。 |
當然,這裏的「一」絕不是普通概念裏的「一」。這個環是原本一個二維的平面經過扭曲後,出現在了三維空間中。假設一個只有二維概念的生物,順著這個環不停地走,即使最後走完全程繞回原點,也只能對路徑的結構做出種種猜測,誠可謂「只緣身在此山中」。 要想理解這「一個面」到底是怎麼回事,必須具備三維的概念,立體地去看它的整體。就好比傳統文化裏講的陰陽,本來就是一體,而並非大眾習慣從局部認識的兩個面。換句話說,只有站在更高層次,才能一眼看懂下面的層次;而在一個層次中要想弄清楚同一層次裏所有的事情,就像莊子說的:「吾生也有涯,而知也無涯。以有涯隨無涯,殆已。」 關於透視學與相對性的問題,對專業人士而言更為重要。美術專業的學生和工作者們在學校裏都學過一些透視法,粗略地講就是利用一些延伸到消失點(Vanishing point)的直線在畫面中勾勒出立體形狀的方法。據說青少年們在圖畫課上也會學一點這些基礎內容,本文就此略過。 
圖例:常規透視法示意圖,學校裏教的透視法一般都是這樣的。 |

圖例:意大利畫家皮薩內洛(Pisanello)所繪的透視圖,25釐米 × 17.5釐米,作於十五世紀。 |
這裏要談的是,這種透視在人的視域中有一個極限。因為人眼對色彩和形狀的感知集中在視野的中心,遠離中心就會讓看到的圖象失真。目前的視覺理論將人的眼球靜止不動時縱向視野的60度範圍定為視野中心;由於人有左右兩隻眼睛,水平方向的角度要稍廣一點。 也就是說,如果所觀察對像的位置超出了視野中心,在透視上就會出現一個相應的扭曲,那麼這時,學校裏教的那些畫直線的透視方法就不準了。這也就是為甚麼美術老師在教學生寫生時,都要學生們與模特或靜物保持一定距離。因為如果靠得太近,物像必然有大量超出視野中心的部份,就會造成畫面的失真。 然而,在實際作畫中,不可能把一切景象都控制在畫家的視野中心,必然會有一部份出現在視野邊緣,就像下面這幅照片一樣。 
圖例:日本大阪市天王寺公園內一景。 |
一些細小的不同於經典透視學的部份暫且不談,只看地面最靠近照片底部的幾條橫向地磚線條,仔細觀察就能發現,它們其實是稍微呈圓弧狀的。而如果根據常規的直線透視法,人們會把它們畫成平行的直線。 這裏就要引入一個比較少見的透視學術語,叫作曲線透視(Curvilinear perspective)。因為人的視網膜本身是半球形的,所以這種透視法更接近人眼看到的圖象,尤其對超出視野中心物像的描繪,比直線透視更為準確。歷史上不少畫家都發現了這一點,也在他們的作品中做過相關嘗試。 
圖例:法國畫家富蓋(Jean Fouquet)的小彩畫《查理四世抵達聖德尼大教堂》(Arrival of Charles IV at the Basilica Saint-Denis),約作於1455年~1460年間。畫家對前景的地板和其它一些地方採用了類似曲線透視的畫法,只是略顯誇張。 |
這些情況也體現了一個道理,就是即使在同一層次中,不同的學術理論也只能在一定的範圍之內起作用,一旦超出這個範圍,它們就不好使了。這時,就需要適用於不同範圍的理論來代替或補充它,才不會被人為地禁錮在某些框架內無法突破。 關於繪畫,還有一種相對而言的情況,就是雖然人們常把繪畫歸類為二維的藝術,但從技術角度看,它其實是三維的。具體說來,多數繪畫都擁有某種「淺三維」的特質,它們除了有長度和寬度,還具備一個較淺的深度。而這裏講的深度並非單純地指向顏料本身的厚度,而是色層間的差異所構造出的一種空間。 我們以一些常用的美術技法來舉例,比如有的畫家畫人物,先把人畫成裸體的,然後用半透明色給人罩上輕柔的衣衫,以此讓服飾顯得合身。這樣,描繪服裝的色料確實是畫在了人物皮膚色料的外層,有一個前後的空間深度。由於顏料的透明度,觀眾也能同時看見內外的色層區別。 
圖例:意大利畫家波提切利(Botticelli)的作品《春》(Primavera),203釐米 × 314釐米,木板坦培拉,約作於1478年~1482年間。作品描繪了神話時代裏的幾位神祇,畫中幾位女神身上透明的白色輕紗薄衣就是用透明和半透明色描繪在皮膚色層之上的。 |
另外,有些表現霧氣、雨景的風景畫也會採用類似畫法。這些技巧能讓畫面展現出一種真實的內外深度,哪怕實際深度或許只有不到半個毫米。 還有一些畫家,由於了解到這種淺三維在人的視覺中也能起作用,因此通過堆砌大量厚重的顏料,把一些油畫、水粉之類的作品畫成了淺浮雕。有人為了表現出立體感和空間感,在畫頭象時把鼻子等凸出的部位畫得很厚,結果造成了畫面嚴重開裂、顏料脫落,反而得不償失。可見,對於藝術理論的運用,也必須與材料的性能結合起來,才能起到它該有的效果。 (待續)
|